Vetores e matrizes

1. $\bigstar$ Escreva um algoritmo que leia um vetor com 10 posições de números inteiros e verifique se um determinado valor, também digitado pelo usuário, está no vetor.

   SOLUçãO: VMPESQUISAVETOR.C.

   SOLUçãO (ALGORITMO): VMBUSCARELEMENTO.ALG

2. $\bigstar$ Escreva um algoritmo que leia um vetor com 10 posições de números inteiros e verifique se um determinado valor, também digitado pelo usuário, está no vetor. Caso o elemento não esteja no vetor, apresente uma mensagem informando tal situação.

   SOLUçãO (ALGORITMO): VMBUSCARELEMENTO2.ALG

3. $\bigstar$ Escreva um algoritmo que leia um vetor com 10 posições de números inteiros e verifique se um determinado valor, também digitado pelo usuário, está no vetor. Se estiver, informe a posição desse elemento no vetor. Caso o elemento não esteja no vetor, apresente uma mensagem informando tal situação.

   SOLUçãO (ALGORITMO): VMBUSCARELEMENTO3.ALG

4. $\bigstar$ Dado um vetor de N números inteiros (N = 20), calcule e escreva o somatório dos valores deste vetor.

   SOLUçãO (ALGORITMO): VMSOMAELEMENTOS.ALG

5. $\bigstar$ Escreva um algoritmo que leia um vetor com 50 posições de números inteiros e mostre somente os positivos.

   SOLUçãO: VMPOSITIVOS.C.

6. $\bigstar$ Escreva um algoritmo que leia dois vetores de 10 posições e faça a multiplicação dos elementos de mesmo índice, colocando o resultado em um terceiro vetor. Mostre o vetor resultante.

   SOLUçãO (ALGORITMO): VMMULTIPLICACAOVETORES.ALG

7. $\bigstar\bigstar$ Escreva um algoritmo que leia um vetor de 80 elementos inteiros. Encontre e mostre o menor elemento e a sua posição.

   SOLUçãO: VMPROCURAMENORELEMENTO.C.

   SOLUçãO (ALGORITMO): VMPROCURAMENORELEMENTO.ALG

8. $\bigstar\bigstar$ Escreva um algoritmo que leia um vetor de 20 posições e mostre-o. Em seguida, troque o primeiro elemento com o último, o segundo com o penúltimo, o terceiro com o antepenúltimo e assim sucessivamente. Mostre o novo vetor depois da troca.

   SOLUçãO (ALGORITMO): VMTROCAVALORES.ALG

9. $\bigstar\bigstar\bigstar$ Escreva um algoritmo que leia um vetor de 13 elementos inteiros, que é o resultado da loteria esportiva, contendo os valores 1 (coluna 1), 2 (coluna 2) e 3 (coluna do meio). Leia a seguir, para cada apostador, o número do seu cartão e um vetor de respostas de 13 posições. Verifique para cada apostador o número de acertos, comparando com o vetor de resultado. Escreva o número do apostador e o número de acertos. Se o apostador tiver 13 pontos, mostrar a mensagem "Ganhador".

10. $\bigstar\bigstar$ Escrever um algoritmo que leia 2 vetores X(10) e Y(10) e os escreva. Crie, a seguir, um vetor para cada operação abaixo:

    a) A união de X com Y.

    b) A diferença entre X e Y.

    c) A soma entre X e Y.

    d) O produto entre X e Y.

    e) A interseção entre X e Y.

    Ao final, escrever o conteúdo de cada operação.

11. $\bigstar$ Escreva um programa que leia valores em um vetor de 5 posições. Escrever os elementos do vetor e após escrever os elementos na ordem inversa.

12. $\bigstar$ Faça um algoritmo que leia um vetor V de 10 posições e, em seguida, verifica se um número N, fornecido pelo usuário, existe no vetor. Se existir, indicar a(s) posição(ões), senão escrever a mensagem "O número fornecido não existe no vetor!".

    SOLUçãO (ALGORITMO): VMBUSCAELEMENTO.ALG

13. $\bigstar$ Faça um algoritmo que leia um vetor K[10] e um vetor N[10]. A seguir, crie um vetor M que seja a diferença entre o vetor K e N (M=K-N). Mostre a seguir o vetor M.

    SOLUçãO (ALGORITMO): VMDIFERENCAVETORES.ALG

14. $\bigstar\bigstar\bigstar$ Escreva um algoritmo que leia um vetor de 15 elementos inteiros. Ordene o vetor em ordem decrescente e exiba-o.

    SOLUçãO (ALGORITMO): VMORDENAVETOR.ALG

15. $\bigstar\bigstar$ Leia um vetor de 12 posições e, em seguida, leia também dois valores X e Y quaisquer correspondentes a duas posições no vetor. Ao final o algoritmo deverá escrever a soma dos valores encontrados entre as respectivas posições X e Y.

16. $\bigstar\bigstar\bigstar$ Faça um algoritmo que leia um vetor de 10 posições. Em seguida, exiba os 3 menores valores do vetor.

17. $\bigstar$ Faça um algoritmo que leia um vetor S[20] e uma variável A. A seguir, mostre o produto da variável escalar A pelo vetor.

    SOLUçãO (ALGORITMO): VMPRODUTOESCALAR.ALG

18. $\bigstar\bigstar\bigstar$ Faça um algoritmo que leia um vetor G[5] que corresponde ao gabarito de uma prova com 5 questões. A seguir, leia uma matriz que contém para cada linha o número de matrícula de cada aluno e cinco respostas (referentes às cinco questões). Para cada aluno, o algoritmo deverá mostrar o seu número de matrícula e a sua respectiva nota. Considere que todas as questões têm o mesmo peso e as respostas possíveis são a, b, c, d ou e.

    SOLUçãO (ALGORITMO): VMRESPOSTAGABARITO.ALG

19. $\bigstar$ Declare um vetor de 10 posições e o preencha com os 10 primeiros números ímpares e, ao final, o escreva.

20. $\bigstar\bigstar$ Faça um algoritmo que leia 2 vetores numéricos A[10] e B[10]. A seguir, crie um vetor C que seja a intersecção de A com B e mostre este vetor C. Obs.: intersecção é quando um valor estiver nos dois vetores. Considere que não há elementos duplicados em cada um dos vetores.

    SOLUçãO (ALGORITMO): VMINTERSECCAOVETORES.ALG

21. $\bigstar$ Faça um algoritmo que leia dois vetores: F[20] e G[20]. Calcule e mostre, a seguir, o produto dos valores de F por G (multiplicar os elementos que possuem mesmo índice).

    SOLUçãO (ALGORITMO): VMPRODUTOVETORES.ALG

22. $\bigstar\bigstar$ Leia um vetor de 16 posições e troque os 8 primeiros valores pelos 8 últimos. Escreva ao final o vetor obtido.

    Solução (algoritmo): VMTrocaPosicoes.alg

23. $\bigstar$ Leia um vetor de 20 posições e em seguida um valor X qualquer. Seu programa deverá fazer uma busca do valor de X no vetor lido e informar a posição em que foi encontrado ou se não foi encontrado.

24. $\bigstar$ Leia um vetor de 40 posições. Contar e escrever quantos valores pares ele possui.

    Solução (algoritmo): VMContaPares.alg

25. $\bigstar\bigstar$ Faça um algoritmo que leia dois vetores de 10 elementos numéricos cada um e intercale os elementos deste em um outro vetor de 20 elementos.

26. $\bigstar\bigstar$ Escreva um programa que leia um vetor de inteiros e positivos e imprima quantas vezes aparece o número 1, 3 e 4, nesta ordem. O vetor terá 100 posições.

27. $\bigstar$ Leia um vetor de 40 posições e atribua o valor 0 para todos os elementos que possuírem valores negativos.

28. $\bigstar\bigstar$ Dados dois vetores, um contendo a quantidade e o outro o preço de 20 produtos, elabore um algoritmo que calcule e exiba o faturamento que é igual a quantidade x preço. Calcule e exiba também o faturamento total que é o somatório de todos os faturamentos, a média dos faturamentos e quantos faturamentos estão abaixo da média.

29. $\bigstar\bigstar$ Faça um programa que leia valores inteiros correspondentes a 90 amostras utilizadas em uma pesquisa (valores entre -400 e 400), armazene-os em um vetor e o escreva. Substitua a seguir todos os valores negativos desse vetor por 999 e escreva o vetor modificado, bem como o número de valores que sofreram substituição.

30. $\bigstar\bigstar\bigstar$ Escreva um algoritmo que calcule a média móvel. O programa deverá executar um laço de leitura de valores inteiros e positivos; a introdução de valores negativos servirá como indicador de término do programa. Para cada valor fornecido deverá ser impressa a média calculada. A média móvel é efetuada sobre um número especificado de pontos. Quando se introduz um novo dado, descarta-se o valor mais antigo dando-se lugar à nova introdução. Este esquema de substituição faz da média móvel um instrumento valioso na análise de tendências. Quanto menor o número de dados, mais sensível será com relação à média. Considerar para a solução deste problema 5 pontos (valores).

31. $\bigstar$ Leia dois vetores de 20 posições e calcule um outro vetor contendo, nas posições pares os valores do primeiro e nas posições ímpares os valores do segundo.

32. $\bigstar$ Dada uma matriz de ordem 4x3 contendo valores numéricos reais. Faça um algoritmo que calcule e exiba a soma dos números positivos e a soma dos números negativos.

    SOLUçãO (ALGORITMO): VMSOMAPOSITIVOSNEGATIVOS.ALG

    SOLUçãO: VMSOMAPOSNEG.C.

33. $\bigstar$ Leia um vetor de 40 posições e acumule os valores do primeiro elemento no segundo, deste no terceiro e assim por diante. Ao final, escreva o vetor obtido.

    Solução (algoritmo): VMAcumuladorValores.alg

34. $\bigstar\bigstar\bigstar$ Leia um vetor contendo letras de uma frase inclusive os espaços em branco. Considere que essa frase terá, no máximo, 20 caracteres. Retirar os espaços em branco do vetor e depois escrevê-lo.

35. $\bigstar\bigstar$ Escreva um programa em C que leia um vetor de 10 valores reais e leia uma matriz 4x4 também com valores reais. O programa deverá imprimir a quantidade de elementos do vetor que são iguais aos elementos da diagonal principal da matriz e quantos elementos da diagonal secundária são menores do que todos os elementos do vetor.

36. $\bigstar\bigstar$ (Prova EST/2010-1) Escreva um programa em C que leia e armazene o código de 50 produtos e os seus respectivos preços. Em seguida, o usuário irá informar o código do produto e a quantidade de solicitada do produto e, então, o programa deverá apresentar o valor a ser pago através da seguinte mensagem: "A compra de <quantidade-solicitada> itens custa <valor-a-ser-pago> reais". Por exemplo, considere que uma caneta custe R$ 2,00 e o usuário queira comprar 50 canetas. Nesse exemplo, o programa deverá apresentar a seguinte mensagem: "A compra de 50 itens custa 100 reais".

37. $\bigstar\bigstar$ (Prova EST/2010-1) Escreva um programa em C que permita que o usuário preencha um vetor de inteiros somente com números ímpares. O usuário poderá também digitar números pares, porém só devem ser considerados os números ímpares no preenchimento. Considere que o vetor terá tamanho igual a 5.

38. $\bigstar\bigstar$ (Prova EST/2010-2) Escreva um algoritmo que leia um vetor chamado VET de 10 inteiros e depois obtenha um vetor RES cujos elementos são os fatoriais respectivos do vetor VET. O usuário irá digitar apenas valores inteiros e positivos. Ao final, imprima o vetor RES. Abaixo segue um exemplo dos valores de entrada e a respectiva resposta.

    Solução (algoritmo): VMCalculaFatorial.alg

    VET

    2

    4

    3

    1

    5

    3

    4

    2

    1

    4

    RES

    2

    24

    6

    1

    120

    6

    24

    2

    1

    24

39. $\bigstar\bigstar\bigstar$ (Prova EST/2010-2) Um quadrado mágico é uma matriz quadrada em que a soma das suas linhas é igual a soma das sua colunas e que também é igual a soma da diagonal principal e da diagonal secundária. A matriz abaixo é um exemplo de quadrado mágico, pois a somatória, em todos os casos, é igual a 15.

    4	9	2
    3	5	7
    8	1	6

    Escreva um algoritmo que leia uma matriz de tamanho 6 x 6 e, ao final, imprima se esta matriz é ou não um quadrado mágico.

    SOLUçãO (ALGORITMO): VMQUADRADOMAGICO.ALG

40. $\bigstar\bigstar$ (Prova EST/2010-2) Escreva um programa na linguagem de programação C em que o usuário preencha uma matriz de tamanho 10 x 5 com valores inteiros. Em seguida, o programa deverá selecionar os valores da matriz que sejam múltiplos de 7 e armazenar esses valores em um vetor. Ao final, imprima o vetor com os valores múltiplos de 7 que estavam na matriz. A interpretação da questão e a forma de solucionar o problema fazem parte da avaliação do exercício.

    SOLUçãO: VMSELECAOMULTIPLOS7.C.

41. $\bigstar\bigstar$ (Prova EST/2011-1) Usando sua matrícula (obrigatório) como entrada, faça o rastreamento do algoritmo abaixo de forma a mostrar o que será impresso como saída do mesmo. Vale ressaltar que o vetor é preenchido com cada número de sua matrícula, na ordem da esquerda para a direita (considere que o número de matrícula é formado por 10 dígitos).

    algoritmo "Provaquest1"
    var
      v:vetor[0..9] de inteiro
      aux,i:inteiro
    inicio
      para i de 0 ate 9 faca
        leia(v[i])
      fimpara
      para i de 9 ate 5 passo -1 Faca
        aux<-v[i]
        v[i]<- v[9-i+1]
        v[9-i+1] <- aux
      fimPara
      v[3]<-v[1]
      v[v[3]]<-v[v[2]]
      para i de 0 ate 9 faca
        escreva(v[i])
      fimpara
    fimalgoritmo
    

42. $\bigstar\bigstar$ (Prova EST/2011-1) Faça um algoritmo para ler uma matriz 100X100 de inteiros positivos. Em seguida, verifique, somente para as linhas pares da matriz, quais os elementos são múltiplos de 5 e coloque-os em um vetor. Ao final imprimir o vetor resultante somente com as posições preenchidas.

    Obs1:O vetor deve ser preenchido sequencialmente.

    Obs2: Não será considerada a resposta em que a verificação for feita ao mesmo tempo da leitura da matriz.

    SOLUçãO (ALGORITMO): VMSELECAOLINHASPARES.ALG

43. $\bigstar\bigstar\bigstar$ (Prova EST/2011-1) Faça um algoritmo para ler uma matriz 100 x 100 de inteiros. Em seguida, nas linhas ímpares, o algoritmo deverá capturar os valores pares encontrados e colocá-los, se existirem, em um vetor (VP) e trocar, na matriz, pelo número 1. Depois, para as linhas pares, o algoritmo deverá capturar os valores ímpares encontrados e colocá-los, se existirem, em um vetor (VI) e trocar, na matriz, pelo número 2. Ao final imprimir a matriz A e os vetores VP e VI (somente com as posições preenchidas).

    SOLUçãO (ALGORITMO): VMSELECAOLINHASPARESIMPARES.ALG

44. $\bigstar$ Dado um valor numérico X e uma matriz A 4x2, elabore um algoritmo que calcule e exiba uma outra matriz B que deverá conter cada elemento da matriz A dividido pelo valor numérico X.

    SOLUçãO (ALGORITMO): VMCALCULAMATRIZB.ALG

45. $\bigstar$ Escreva um algoritmo que leia dois vetores de tamanho igual a 5 e verifique se estes são palíndromos. Palíndromo é uma palavra, frase ou qualquer sequência de unidades que tenha a propriedade de poder ser lida tanto da direita para esquerda, como da esquerda para a direita e o conteúdo é o mesmo.

    Exemplos: ARARA ou RADAR ou MIRIM - são palíndromos.

    SOLUçõES: VMTESTAPALINDROMO.C OU VMTESTAPALINDROMO2.C.

    Só como curiosidade, o maior palídromo do mundo possui 17.259 palavras. O texto desse palíndromo pode ser encontrado no endereço: http://www.norvig.com/pal2txt.html. Já imaginaram criar um programa em C para testar? Fica aí o desafio.

46. $\bigstar\bigstar$ Existem palíndromos de frases inteiras e não apenas de palavras. Por exemplo, a frase A droga da gorda é um exemplo de palíndromo (desconsiderando os espaços em branco, é claro). Assim, escreva um algoritmo que leia uma frase de no máximo 20 caracteres e informe se esta frase é um palíndromo (desconsidere os espaços em branco, como o exemplo mencionado).

47. $\bigstar\bigstar$ Escreva um algoritmo que leia duas palavras de tamanho 5 e verifique se estas são anagramas. Um anagrama é uma espécie de jogo de palavras, resultando do arranjo das letras de uma palavra ou frase para produzir outras palavras, utilizando todas as letras originais exatamente uma vez. Diferentemente dos palíndromos, o arranjo não precisa ser igual, pois todo palíndromo é um anagrama, mas nem todo anagrama é um palíndromo.

    Exemplos de anagrama: Célia e Alice ou Lyseu e Suely.

    SOLUçãO (ALGORITMO): VMTESTAANAGRAMA.ALG

    SOLUçãO (ALGORITMO): VMTESTAANAGRAMA2.ALG

48. $\bigstar\bigstar$ Escreva um algoritmo que leia 3 vetores de 9 posições e crie um outro vetor que deverá ser formado com o 1º terço do primeiro, o 2º terço do segundo e o último terço do 3º. Escrever o vetor resultante ao final.

49. $\bigstar\bigstar$ Faça um algoritmo que leia um vetor S[20]. A seguir, compacte este vetor S, retirando todos os valores nulos ou negativos e mostre então o vetor compactado.

    Solução (algoritmo): VMCompactaVetor.alg

50. $\bigstar\bigstar$ Faça um algoritmo que leia um vetor T[15]. Crie, a seguir, um vetor Fat[15] que contém os fatoriais do vetor T. Mostre, a seguir, o vetor Fat.

    Solução (algoritmo): VMVetordeFatoriais.alg

51. $\bigstar\bigstar$ Leia um vetor de 10 posições e verifique se existem valores iguais (repetidos) e os escreva.

52. $\bigstar\bigstar$ Faça um algoritmo que leia um vetor V[10] e o escreva. Crie, a seguir, um vetor COMP que conterá somente os valores não repetidos de V. Mostre então o vetor COMP.

53. $\bigstar\bigstar$ Escreva um algoritmo que receba o nome de cinco clientes e armazene-os em um vetor. Em um segundo vetor, armazene a quantidade de DVDs locados em 2010 por cada um dos cinco clientes. Sabe-se que, para cada dez locações, o cliente tem direito a uma locação grátis. O algoritmo deverá mostrar todos os nomes dos clientes com a quantidade de locação grátis que ele tem direito.

    SOLUçãO (ALGORITMO): VMLOCADORADVD.ALG

54. $\bigstar\bigstar$ Faça um algoritmo que leia um vetor V[10] e um vetor X[10]. A seguir, crie um vetor Y[20] que conterá os valores dos vetores V e X em ordem crescente. Obs.: o método para deixar o vetor resultante ordenado é livre.

55. $\bigstar\bigstar\bigstar$ Leia um vetor de 50 posições e o compacte, ou seja, elimine as posições com valor zero avançando uma posição com os valores subseqüentes do vetor. Dessa forma todos os zeros devem ficar para nas posições finais do vetor.

56. $\bigstar\bigstar\bigstar$ Faça um algoritmo que gere os 10 primeiros números primos acima de 100 e armazene-os em um vetor X[10]. Ao final do algoritmo, mostre então o vetor X.

    SOLUçãO (ALGORITMO): VMGERAVETOR10PRIMOS.ALG

57. $\bigstar\bigstar$ Dado um vetor com N elementos numéricos reais positivos obter a maior diferença, em termos absolutos, entre dois elementos consecutivos neste vetor. Considere que N é igual a 6.

    SOLUçãO (ALGORITMO): VMMAIORDIFERENCA.ALG

58. $\bigstar\bigstar$ Faça um algoritmo que leia um vetor K[30]. Troque a seguir, todos os elementos de ordem ímpar do vetor com os elementos de ordem par imediatamente posteriores. Mostre o vetor modificado.

59. $\bigstar$ Faça um algoritmo que leia um vetor N[20]. A seguir, encontre o menor elemento do vetor N e a sua posição dentro do vetor, mostrando a seguinte mensagem: O menor elemento de N é ? e sua posição dentro do vetor é: ?.

60. $\bigstar\bigstar$ Criar um programa que leia uma matriz 5x5 e armazene no Vetor A o maior elemento de cada coluna da matriz e no Vetor B o menor elemento de cada coluna da matriz. Apresentar como resultado o vetor A, o vetor B e a média dos valores de cada vetor.

61. $\bigstar$ Escreva um algoritmo que leia e mostre um vetor de 20 elementos inteiros. A seguir, conte quantos valores pares existem no vetor.

62. $\bigstar\bigstar$ Faça um algoritmo que leia um vetor N[20]. Troque a seguir o primeiro elemento com o último, o segundo elemento com o penúltimo, etc., até trocar o décimo com o décimo primeiro. Mostre o vetor modificado.

63. $\bigstar\bigstar$ Considere um vetor de trajetórias de 9 elementos, onde cada elemento possui o valor do próximo elemento do vetor a ser lido.

    Índice	1	2	3	4	5	6	7	8	9
    Valor	5	7	6	9	2	8	4	0	3

    Assim, a seqüência da leitura seria 1, 5, 2, 7, 4, 9, 3, 6, 8, 0. Faça um algoritmo que seja capaz de ler esse vetor e seguir a trajetória.

64. $\bigstar\bigstar$ Leia uma matriz 10 x 10 e escreva a localização (linha e a coluna) do maior valor. Considere que a matriz não terá elementos repetidos.

    SOLUçãO (ALGORITMO): VMBUSCAMAIORVALORMATRIZ.ALG

65. $\bigstar\bigstar$ Modifique a resposta do exercício anterior e faça um algoritmo considerando que a matriz poderá ter elementos repetidos.

66. $\bigstar\bigstar$ Escreva um programa na linguagem de programação C em que o usuário preencha uma matriz de tamanho 10x5 com valores inteiros. Em seguida, o programa deverá selecionar os valores da matriz que sejam múltiplos de 7 e armazenar esses valores em um vetor. Ao final, imprima o vetor com os valores múltiplos de 7 que estavam na matriz.

    SOLUçãO: VMMULTIPLOS7.C.

67. $\bigstar$ Declare uma matriz 5 x 5. Preencha com 1 a diagonal principal e com 0 os demais elementos. Escreva, ao final, a matriz obtida.

    SOLUçãO (ALGORITMO): VMPREENCHEDIAGONALPRINCIPAL.ALG

68. $\bigstar\bigstar$ Leia duas matrizes 4 x 4 e escreva uma terceira com os maiores elementos entre as duas primeiras em cada posição equivalente.

    SOLUçãO: VMCOMPARAMATRIZES.C.

69. $\bigstar\bigstar$ Escreva um algoritmo que leia uma matriz de inteiros de ordem 4 e verifique se a soma dos elementos das diagonais são iguais.

    SOLUçãO (ALGORITMO): VMSOMAIGUALDIAGONAIS.ALG

70. $\bigstar$ Leia uma matriz 6 x 6, conte e escreva quantos valores maiores que 10 ela possui.

71. $\bigstar\bigstar$ Escrever um algoritmo que lê uma matriz M(5,5) e cria 2 vetores SL(5) e SC(5) que contenham, respectivamente, as somas das linhas e das colunas de M. Escrever a matriz e os vetores criados.

    SOLUçãO (ALGORITMO): VMSOMALINHASCOLUNAS.ALG

72. $\bigstar\bigstar$ Leia uma matriz 20 x 20. Leia também um valor X. O programa deverá fazer uma busca desse valor na matriz e, ao final, escrever a localização (linha e coluna) ou uma mensagem de "Elemento não encontrado". Considere que a matriz não possui elementos repetidos.

    Solução (algoritmo): VMBuscaElementoMatriz.alg

73. $\bigstar\bigstar$ Leia uma matriz 4 x 4 e troque os elementos da 1ª linha pelos elementos da 4ª coluna. Escrever, ao final, a matriz transformada.

    SOLUçãO (ALGORITMO): VMTROCALINHAPORCOLUNA.ALG

74. $\bigstar\bigstar$ Desenvolver um algoritmo que leia os elementos da 1ª linha de uma matriz 4x4 numérica e, a partir desses elementos, calcule e mostre os outros elementos da matriz. Sabe-se que os elementos da 2ª linha são os elementos da 1ª linha x 2, os elementos da 3ª linha são os elementos da 1ª linha x 3 e assim por diante. Ao final, imprima a matriz calculada.

75. $\bigstar\bigstar$ Leia uma matriz 8 x 8 e a transforme numa matriz triangular inferior. Ao final, escreva a matriz transformada.

    SOLUçãO (ALGORITMO): VMTRANSFORMAMATRIZTRIANGULARINFERIOR.ALG

    Obs.: matriz triangular inferior é aquela em que todos os seus elementos acima da diagonal principal são iguais a zero.

76. $\bigstar\bigstar\bigstar$ Dada uma matriz A (numérica) de tamanho 3x3, desenvolva um algoritmo que gere uma outra matriz B de tamanho 3x4. A matriz B tem os mesmos elementos da matriz B quando os elementos tiverem os mesmos índices. A quarta coluna de B corresponderá à média aritmética dos elementos da sua respectiva linha. Ao final, imprima a matriz B.

    SOLUçãO (ALGORITMO): VMMEDIAARITMETICAMATRIZ.ALG

77. $\bigstar\bigstar$ Leia uma matriz 5 x 5 e faça uma troca entre as diagonais principal e secundária. Escreva-a ao final.

78. $\bigstar$ Leia duas matrizes 10 x 10 e faça uma substituição entre a diagonal inferior da primeira com a diagonal superior da segunda.

79. $\bigstar\bigstar$ Dada uma matriz MAT de dimensão 2x3 contendo números inteiros positivos, faça um algoritmo que gere uma matriz XIS de caracteres, tal que se o número da posiçãode MAT[i][j] for par o elemento correspondente na matriz XIS[i][j] deverá conter a informação P, caso contrário deverá conter a informação I. Exibir as duas matrizes.

80. $\bigstar\bigstar\bigstar$ Faça um algoritmo que leia um vetor G[13] que é o gabarito de um teste da loteria esportiva, contendo os valores 1 quando for coluna 1, 0 quando for coluna do meio e 2 quando for coluna 2. A seguir, o algoritmo deverá ler as apostas de 10 jogadores, incluindo o número do cartão de cada apostador e um vetor R[13] que seriam as respostas dos apostadores. Para cada apostador, mostre o número de acertos.

81. $\bigstar\bigstar\bigstar$ Com relação ao exercício anterior, calcule e mostre o percentual dos apostadores que fizeram de 10 a 13 pontos e o percentual dos apostadores que fizeram menos de 10 pontos.

82. $\bigstar\bigstar\bigstar$ Escreva um programa que carregue uma matriz 12 x 4 com os valores das vendas de cadeiras, onde cada linha representa um mês do ano e cada coluna representa uma semana do mês. Calcule e mostre:
    • O total vendido em cada mês do ano, mostrando o nome do mês por extenso.
    • O total vendido em cada semana durante todo o ano.
    • O total vendido pela loja no ano.

83. $\bigstar\bigstar$ Leia uma matriz 8 x 8 e escreva o maior elemento da diagonal principal e a soma dos elementos da diagonal secundária.

    Solução (algoritmo): VMOperacoesMatriz.alg

84. $\bigstar\bigstar\bigstar$ Leia uma matriz M[5,5]. A seguir, ordene os elementos da matriz M e mostre como ficou a matriz ordenada, linha por linha.

85. $\bigstar$ Escreva um algoritmo que lê uma matriz M[5,5]. Substitua, a seguir, todos os valores negativos da matriz pelo seu módulo. Exemplo: substitua -2 por 2, -16 por 16, assim por diante. Ao final, imprima a matriz modificada.

86. $\bigstar\bigstar$ Escreva um algoritmo que leia uma matriz N x M do usuário e a transforme em um vetor unidimensional. Ao final, imprima os valores através do vetor. Considere que N vale 2 e M vale 3.

87. $\bigstar$ Faça um algoritmo que calcule a média dos elementos da diagonal principal de uma matriz 10 X 10 de números.

    SOLUçãO (ALGORITMO): VMMEDIADIAGONALPRINCIPAL.ALG

88. $\bigstar$ Faça um algoritmo que calcule a média dos elementos da diagonal secundária de uma matriz 10 X 10 de números.

    SOLUçãO: VMMEDIADIAGSECUNDARIA.C.

89. $\bigstar\bigstar$ Faça um algoritmo que gere a seguinte matriz:

    1	3	3	3	3	2
    3	1	3	3	2	3
    3	3	1	2	3	3
    3	3	2	1	3	3
    3	2	3	3	1	3
    2	3	3	3	3	1

    SOLUçãO (ALGORITMO): VMIMPRIMEMATRIZ.ALG

    SOLUçãO (ALGORITMO): VMIMPRIMEMATRIZ2.ALG

90. $\bigstar\bigstar$ Faça um algoritmo que gere a seguinte matriz:

    1	1	1	1	1	1
    1	2	2	2	2	1
    1	2	3	3	2	1
    1	2	3	3	2	1
    1	2	2	2	2	1
    1	1	1	1	1	1

    SOLUçãO: VMIMPRIMEMATRIZQUADRADA.C.

91. $\bigstar\bigstar$ Faça um algoritmo que leia uma matriz 20x15 de números. Calcule e mostre a soma das linhas pares da matriz.

    SOLUçãO (ALGORITMO): VMSOMALINHASPARES.ALG

    SOLUçãO (ALGORITMO): VMSOMALINHASPARES2.ALG

92. $\bigstar\bigstar$ Na teoria dos sistemas, define-se como elemento minimax de uma matriz o menor elemento da linha onde se encontra o maior elemento da matriz. Escreva um algoritmo que leia uma matriz 10 X 10 de números e encontre seu elemento minimax, mostrando também sua posição.

93. $\bigstar\bigstar$ Faça um algoritmo que leia uma matriz 50x50 de números. A seguir, multiplique cada linha pelo elemento da diagonal principal daquela linha. Mostre a matriz após as multiplicações.

94. $\bigstar\bigstar$ Escreva um algoritmo que leia uma matriz 6 x 6 e atribua o valor 0 para os valores negativos encontrados fora das diagonais principal e secundária.

    SOLUçãO (ALGORITMO): VMMATRIZPRINCIPALSECUNDARIA.ALG

95. $\bigstar\bigstar\bigstar$ Faça um programa lê uma matriz A com 7 x 7 números e depois crie 2 vetores ML(7) e MC(7), que contenham, respectivamente, o maior elemento de cada uma das linhas e o menor elemento de cada uma das colunas. Escrever a matriz A e os vetores ML e MC.

96. $\bigstar\bigstar$ Leia uma matriz 50 x 2, onde cada coluna corresponde a um lado de um triangulo retângulo. Declare um vetor que contenha a área dos respectivos triângulos e o escreva.

    SOLUçãO (ALGORITMO): VMCALCULAAREARETANGULO.ALG

97. $\bigstar\bigstar$ Elabore um algoritmo para preencher uma matriz quadrada de tamanho 4x4. Depois crie uma outra matriz que seja o resultado da divisão dos elementos de cada linha pelo respectivo elemento da diagonal principal. Ao final o algoritmo deverá exibir as duas matrizes.

    SOLUçãO (ALGORITMO): VMDIVIDEMATRIZ.ALG

98. $\bigstar\bigstar\bigstar$ Uma empresa possui ônibus com 48 lugares divididos em lado direito e lado esquerdo. Faça um algoritmo que utilize duas matrizes 12 x 2 para controlar as poltronas ocupadas no lado direito (janela e corredor) e no lado esquerdo (janela e corredor). As poltronas serão referenciadas conforme sua numeração. As poltronas ocupadas serão apresentadas com o número zero. Inicialmente todas as poltronas estarão livres. O algoritmo terá as seguintes opções:

    a) Mostrar poltronas.

    b) Vender passagens.

    c) Sair.

99. $\bigstar\bigstar$ Escreva um algoritmo para gerenciar a venda de ingressos das poltronas numeradas de um teatro que tem 100 lugares. Para cada nova reserva deve ser verificado se o assento se encontra disponível.

100. $\bigstar\bigstar$ Leia duas matrizes 20 x 20 e escreva os valores da primeira que ocorrem em qualquer posição da segunda matriz.

     SOLUçãO (ALGORITMO): VMCOMPARAMATRIZES.ALG

101. $\bigstar\bigstar\bigstar$ Refaça o exercício anterior, mas agora sem imprir números repetidos. Por exemplo, se o número 2 aparecer várias vezes nas duas matrizes, deve-se imprimi-lo apenas uma única vez. Essa regra deve valer para a matriz inteira.

102. $\bigstar\bigstar\bigstar$ Leia uma matriz 100 x 10 que se refere às respostas de 10 questões de múltipla escolha, referentes a 100 alunos. Leia também um vetor de 10 posições contendo o gabarito das respostas que podem ser a, b, c ou d. Seu programa deverá comparar as respostas de cada candidato com o gabarito e emitir um vetor Resultado, contendo a pontuação correspondente.

103. $\bigstar\bigstar\bigstar$ (Prova monitoria UEA/2011) Escreva um algoritmo que leia 5 caracteres digitados pelo usuário e os armazene em um vetor. Considere que o usuário não irá digitar valores repetidos. Depois disso, o usuário irá preencher uma matriz de tamanho 3x2 de caracteres. Considere, novamente, que o usuário não irá digitar caracteres repetidos na matriz. Em seguida, o algoritmo deve verificar e escrever na tela se os 5 caracteres digitados inicialmente estão na matriz. Se todos os caracteres estiverem na matriz, o algoritmo deve exibir a posição de cada caractere na matriz.

     SOLUçãO (ALGORITMO): VMPROCURACARACTERES.ALG

104. $\bigstar\bigstar$ Faça um programa que leia 6 números de 5 apostadores e ao final da leitura de todos os números dos 5 apostadores exiba a posição da matriz ou as posições da matriz que possui o menor valor.

     SOLUçãO (ALGORITMO): VMAPOSTADORESMATRIZ.ALG

105. $\bigstar\bigstar$ Escrever um algoritmo que lê 10 valores quaisquer, armazenando em um vetor. Contar quantos deles estão no intervalo [10,20] e quantos deles estão fora deste intervalo, mostrando estas informações.

     SOLUçãO (ALGORITMO): VMINTERVALOVALORES.ALG

106. $\bigstar\bigstar$ Escrever um algoritmo que lê 30 valores inteiros em um intervalo de 0 a 100, armazenando em um vetor. Contar quantos deles estão em cada um dos intervalos [0,25], [25,50], [50,75], [75,100].

     SOLUçãO (ALGORITMO): VMINTERVALOGRUPOVALORES.ALG

107. $\bigstar\bigstar$ Escrever um algoritmo semelhante ao anterior que calcula as médias aritméticas de cada intervalo e as mostra, juntamente com o número de valores encontrados em cada intervalo.

     SOLUçãO (ALGORITMO): VMINTERVALOGRUPOVALORESMEDIA.ALG

108. $\bigstar\bigstar$ Faça um programa que carregue um vetor de nove elementos numéricos inteiros, calcule e mostre os números primos e suas respectivas posições.

109. $\bigstar$ Leia um vetor de 100 elementos reais e verifique se existem elementos iguais a 64. Se existirem, escreva as posições em que estão armazenados.

110. $\bigstar$ Dadas as matrizes A e B de tamanho 5 x 3, determine a matriz C = A + B. Imprima A, B e C.

     SOLUçãO (ALGORITMO): VMSOMAMATRIZES.ALG

111. $\bigstar\bigstar\bigstar$ Dada uma matriz de dimensão 3x6, calcule a soma de cada coluna dessa matriz e armazene esses valores num vetor. Imprima a matriz e o vetor.

     SOLUçãO (ALGORITMO): VMSOMACOLUNASMATRIZ.ALG

112. $\bigstar$ Dadas as matrizes A e B, determine a matriz C tal que C = A * B. Imprima A, B e C.

113. $\bigstar\bigstar$ Dada a matriz A de dimensão 4x4 de elementos inteiros, calcule e imprima a soma dos elementos situados abaixo da diagonal principal de A, incluindo os elementos da própria diagonal principal.

     SOLUçãO (ALGORITMO): VMSOMAELEMENTOSMATRIZ.ALG

114. $\bigstar\bigstar\bigstar$ Faça um programa que receba a quantidade de peças vendidas por um vendedor e armazene essas quantidades em um vetor (considere que serão digitados 10 tipos diferentes de peças). Receba também o preço da peça vendida de cada vendedor e armazene esses preços em outro vetor. Existem apenas dez vendedores e cada vendedor pode vender apenas um tipo de peça, isto é, para cada vendedor existe apenas um preço. Calcule e mostre a quantidade total de peças vendidas por todos os vendedores e para cada vendedor calcule e mostre o valor total da venda, isto é, a quantidade de peças * o preço da peça.

115. $\bigstar$ Leia um vetor de 50 elementos do tipo caracter e verifique se existem elementos iguais a um determinado caracter fornecido pelo usuário. Se existirem escreva as posições em que estão armazenados.

116. $\bigstar\bigstar\bigstar$ Dada uma matriz 10x3 com as notas de 10 alunos em 3 provas, faça um programa que mostre um relatório com o número do aluno (número da linha) e a prova em que cada aluno obteve menor nota. Ao final do relatório, mostre quais alunos tiveram a menor nota na P1, quais alunos tiveram a menor nota na P2 e quais alunos tiveram a menor nota na P3.

117. $\bigstar\bigstar$ Faça um algoritmo que leia 2 vetores A[10] e B[10]. A seguir, crie um vetor C que seja a intersecção de A com B e mostre este vetor C. Obs.: intersecção é quando um mesmo valor estiver nos dois vetores. Considere que não há elementos duplicados em cada um dos vetores.

     SOLUçãO (ALGORITMO): VMINTERSECCAOVETORES.ALG

118. $\bigstar\bigstar\bigstar\bigstar$ Escreva um algoritmo para simular o jogo da velha (permita que duas pessoas possam entrar com as jogadas).

119. $\bigstar$ Construir um algoritmo que efetue a leitura, a soma e a impressão do resultado entre duas matrizes inteiras que comportem 25 elementos.

     SOLUçãO: VMSOMAMATRIZES.C.

120. $\bigstar\bigstar$ Elaborar um algoritmo que leia duas matrizes inteiras, A e B, do tipo (3x3) e calcule em uma matriz R a sua multiplicação, ou seja, R=A*B.

121. $\bigstar$ Desenvolver um algoritmo estruturado em pseudocódigo para ler uma matriz qualquer, considerando que esta matriz tenha o tamanho de 4 linhas por 5 colunas. Ao final deve ser apresentado os valores.

     SOLUçãO: VMLEIMPRIMEMATRIZ.C.

122. $\bigstar\bigstar$ Desenvolver um algoritmo estruturado em pseudocódigo para ler duas matrizes A e B cada uma com uma dimensão e 7 elementos. Construir uma matriz C de duas dimensões, onde a primeira coluna deverá ser formada pelos elementos da matriz A e a segunda coluna deverá ser formada pelos elementos da matriz B. Apresentar o resultado da matriz C.

     SOLUçãO: VMJUNTAMATRIZES.C.

123. $\bigstar$ Escreva um algoritmo que leia um vetor inteiro de 30 posições e crie um segundo vetor, substituindo os valores nulos por 1. Mostre os 2 vetores.

     SOLUçãO: VMELIMINANULOS.C.

124. $\bigstar\bigstar$ (Prova EST/2011-3) Escreva um programa em C que leia uma matriz de tamanho 50 x 50. Após a matriz preenchida, o programa deverá exibir a soma dos elementos da segunda linha e a soma dos elementos da diagonal principal.

     SOLUçãO: VMIMPRIMELINHADIAGONAL.C.

125. $\bigstar\bigstar$ Dado o seguinte vetor:

     
     
     

     Qual será a sua configuração depois de ser executado os comandos:

     para I de 8 ate 5 passo -1 faca
       AUX <- VET[I]
       VET[I] <- VET[8-I+1]
       VET[8-I+1] <- AUX
     fimpara
     VET[3] <- VET[1]
     VET[VET[3]] <- VET[VET[2]]
     

126. $\bigstar$ Dado o seguinte vetor de caracteres:
     $$VET = \left[\begin{array}{c\vert c\vert c\vert c\vert c\vert c\ve... ...\vert c\vert c\vert c} T & R & X & S & & E & O & B & A & ! \end{array} \right]$$

     Qual será a sua configuração depois de ser executado os comandos:

      AUX <- VET[6]
      VET[6] <- VET[9]
      VET[9] <- AUX
      para I de 1 ate 4 passo 1 faca
       AUX <- VET[I]
       VET[I] <- VET[9-I]
       VET[9-I] <- AUX
      fimpara
      VET[6] <- VET[2]
     

127. $\bigstar\bigstar$ Criar um algoritmo que armazene dados inteiros em uma matriz de ordem cinco e imprima toda a matriz e uma outra matriz formada pelos números que se encontram em posição cuja linha mais coluna formam um número par.

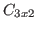128. $\bigstar\bigstar$ Crie um algotimo que leia uma matriz $C_{3x2}$ e que gere a transposta da matriz C, ou seja 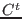$C^t$. A matriz transposta é gerada trocando linha por coluna.

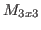129. $\bigstar\bigstar$ Criar um algoritmo que leia uma matriz $M_{3x3}$ e imprima uma outra matriz, conforme mostrado a seguir:
     $$\left[\begin{array}{rrr} 1&2&3\\ 4&5&6\\ 7&8&9 \end{array}\righ... ...arrow\quad \left[\begin{array}{rrr} 7&4&1\\ 8&5&2\\ 9&6&3 \end{array}\right]$$

130. $\bigstar\bigstar\bigstar$ Utilizando os algoritmos a seguir responda as questôes:

     Algoritmo 1:
     Var

     A: vetor [1..10] de inteiro
     B: vetor [1..10,1..10] de inteiro
     i,j,soma1,soma2: inteiro
     

     inicio

       leia(A,B)
       soma1 <- 0
       soma2 <- 0
       para i de 1 ate 10 faca
         para j de 1 ate 10 faca
           soma1 <- soma1 +A[i]
           soma2 <- soma2 +B[i,j]
          fimpara
        fimpara
       escreva(soma1,soma2)
     fimalgoritmo
     

     Algoritmo 2:
     Var

     A: vetor [1..10] de inteiro
     B: vetor [1..10,1..10] de inteiro
     i,j,soma1,soma2: inteiro
     

     inicio

       leia(A,B)
       soma1 <- 0
       soma2 <- 0
       para i de 1 ate 10 faca
         soma1 <- soma1+A[i]
         para j de 1 ate 10 faca
           soma2 <- soma2 +B[i,j]
         fimpara
       fimpara
       escreva(soma1,soma2)
     fimalgoritmo
     

     Responda:

     1. O que executa cada algoritmo?
     2. Os dois algoritmos fornecem as mesmas respostas?
     3. No primeiro algoritmo, quantas vezes são executados os comandos:
        • soma1 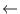$\leftarrow$ soma1 + A[i]
        • soma2 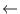$\leftarrow$ soma2 + B[i,j]
     4. No segundo algoritmo, quantas vezes são executados os comandos:
        • soma1 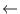$\leftarrow$ soma1 + A[i]
        • soma2 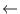$\leftarrow$ soma2 + B[i,j]
     5. Qual o algoritmo mais eficiente? Justifique a sua resposta.

131. $\bigstar\bigstar\bigstar\bigstar$ Escreva um algoritmo que leia uma matriz quadrada de ordem 3 com valores numéricos. Essa matriz será preenchida pelo usuário. Considerando as regras do Sodoku, o algoritmo deverá imprimir uma mensagem informando se a matriz atende ou não às regras do jogo.

132. $\bigstar\bigstar$ (Prova UEA/2012.1) Faça um algoritmo que leia um vetor de 100 posições de valores numéricos. Depois da leitura, multiplique todos seus elementos pelo primeiro número primo encontrado no vetor. Se não houver número primo no vetor não altere os seus valores. Mostre o vetor após o processamento.

     SOLUçãO (ALGORITMO): VMMULTIPLICAPORPRIMOS.ALG

133. $\bigstar\bigstar\bigstar$ (Prova UEA/2012.1) Escreva um algoritmo que leia uma matriz A de tamanho 3x3 com valores numéricos. Depois o algoritmo deverá imprimir uma mensagem informando quantos elementos dessa matriz pertencem à série de Fibonacci. A série de Fibonacci tem os dois primeiros elementos iguais a 1 e os demais elementos são gerados a partir da soma dos dois últimos elementos. Portanto, o primeiro elemento é igual a 1. O segundo elemento é igual a 1. O terceiro elemento é igual a 2 (1+1). O quarto elemento é igual a 3 (1+2). O quinto elemento é igual 5 (2+3). E assim teríamos a seguinte série: 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

     SOLUçãO (ALGORITMO): VMCONTADORSERIEFIBONACCI.ALG

134. $\bigstar$ Escreva um algoritmo que realize a leitura de um vetor e dos salários pagos a um indivíduo durante um ano. Em seguida, o algoritmo deverá mostrar os valores mensais e o total anual.

135. $\bigstar$ Escreva um algoritmo que solicite ao usuário um número. Em seguida, atribua a um vetor todos os números inteiros a partir desse número, exceto os múltiplos de 3. Quando encontrar o primeiro múltiplo de 100 o algoritmo é interrompido.

136. $\bigstar\bigstar$ Ler dois vetores A e B com 10 elementos. O vetor A deverá aceitar apenas a entrada de valores que sejam divisíveis por 2 e 3, enquanto o vetor B deverá aceitar apenas a entrada de valores que sejam múltiplos de 5. A entrada dos vetores deverá ser validada pelo algoritmo e não pelo usuário. Construa um vetor C que seja a junção dos vetores A e B, de modo que o vetor C contenha 20 elementos. Ao final, apresentar a matriz C.

137. $\bigstar\bigstar$ Faça um algoritmo que leia duas matrizes A e B com 15 elementos cada. Construir duas outras matrizes C e D de mesmo tipo, sendo que cada elemento da matriz C deverá ser o quadrado do elemento correspondente da matriz A, e cada elemento da matriz D deverá ser o fatorial do elemento correspondente da matriz B. Em seguida construir uma matriz E, que deverá conter a diferença dos elementos das matrizes C e D multiplicado com a soma dos elementos das matrizes A e B. Apresentar os elementos da matriz E.

138. $\bigstar\bigstar$ Ler duas matrizes A e B de duas dimensões com 5x5. A matriz A deverá ser formada por valores que não sejam divisíveis por 3, enquanto a matriz B deverá ser formada por valores que não sejam divisíveis por 2. As entradas dos valores nas matrizes deverão ser validadas pelo algoritmo. Construir a matriz C, de mesmo tamanho, onde cada elemento de C é a divisão entre os elementos correspondentes de A e B.

139. $\bigstar\bigstar$ Faça um algoritmo que leia quatro vetores A, B, C e D de tamanho 4. Construir uma matriz E de duas dimensões 4x4, sendo que a primeira linha da matriz E deverá ser formada pelo quadrado dos valores dos elementos da matriz A, a segunda linha da matriz E deverá ser formada pelo cubo dos valores dos elementos da matriz B, a terceira linha da matriz E deverá ser formada pelo quádruplo dos valores dos elementos da matriz C e a quarta linha da matriz E deverá ser formada pelo fatorial dos valores dos elementos da matriz D. Imprima a matriz E.

140. $\bigstar\bigstar$ Um elemento Aij de uma matriz é dito ponto de cela da matriz A se, e somente se, Aij for ao mesmo tempo o menor elemento da linha i e o maior elemento da coluna j. Faça um programa que carregue uma matriz de ordem 5 x 7, verifique se a matriz possi ponto de sela e, se possuir, mostre seu valor e sua localização.

141. $\bigstar\bigstar$ Crie um programa que preencha uma matriz 8 x 8 com números inteiros e mostre uma mensagem dizendo se a matriz digitada é simétrica. Uma matriz só pode ser considerada simétrica se A[i,j] = A[j,i]

     SOLUçãO: VMTESTAMATRIZSIMETRICA.C.

142. $\bigstar\bigstar\bigstar$ Faça um programa que receba:
     • um vetor com o nome de cinco cidades diferentes;
     • uma matriz 5 x 5 com a distância entre as cidades, sendo que na diagonal principal deve ser colocada automaticamente distância zero, ou seja, não deve ser permitida a digitação;
     • o consumo de combustível de um veículo, ou seja, quantos quilômetros este veículo percorre com um litro de combustível.

     O programa deverá calcular e mostrar:

     • os percursos que não ultrapassam 250 quilômetros (os percursos são compostos pelos nomes das cidades de origem e pelos nomes das cidades de destino);
     • todos os percusos (nome da cidade de origem e nome da cidade de destino), juntamente com a quantidade de combustível necessária para o veículo percorrê-los;

143. $\bigstar\bigstar\bigstar$ Faça um programa que utilize uma matriz 5 x 5 que aceite três tipo de valores: múltiplos de 5, múltiplos de 11 e múltiplos de 13. Devem ser lidos apenas valores maiores que zero. Após a leitura, os números devem ser distribuídos da seguinte maneira:
     • os múltiplos de 5 devem ocupar a diagonal principal;
     • os múltiplos de 11 devem ficar acima da diagonal principal;
     • os múltiplos de 13 devem ficar a baixo da diagonal principal;

     Como alguns números podem ser múltiplos de 5, de 11 e também de 13 (por exemplo, 55 é múltiplo de 5 e de 11; 65 é múltiplo de 5 e de 13), deve-se primeiro, verificar se o número digitado é múltiplo de 5. Caso não seja, deve-se verificar se é múltiplo de 11. Caso não seja, deve-se verificar se pe múltiplo de 13. Caso não seja, o programa deverá mostrar a mensagem: ``Número inválido'' (por exemplo 55 deverá ser considerado múltiplo de 5, pois essa é a comparação que será feita primeiro).

     Segue-se um exemplo:

     $$\left[\begin{array}{r\vert r\vert r\vert r\vert r}\hline 5&44&11&... ... \hline 52&78&65&40&132 \hline 91&117&104&143&25 \hline \end{array}\right]$$

     SOLUçãO (ALGORITMO): VMPREENCHEMATRIZESPECIAL.ALG

144. $\bigstar\bigstar\bigstar$ Elabore um programa que preencha uma matriz 12 x 4 com os valores das vendas de uma loja, em que cada linha representa um mês do ano e cada coluna representa uma semana do mês. O programa deverá calcular e mostrar:
     • o total vendido em cada mês do ano, mostrando o nome do mês por extenso;
     • o total vendido em cada semana durante todo o ano;
     • o total vendido pela loja no ano;

145. $\bigstar\bigstar$ Elabore um programa que preencha uma matriz 4 x 5, calcule e mostre um vetor com cinco posições, onde cada posição contém a soma dos elementos de cada coluna da matriz. O programa deverá mostrar apenas os elementos do vetor maiores que dez. Se não existir nenhum elemento maior que dez, deverá mostrar uma mensagem.

146. $\bigstar\bigstar$ Faça um programa que receba os preços de vinte produtos em cinco lojas diferentes e armazene-os em uma matriz 20 x 5. Desconsiderando empates, o programa deverá mostrar o número do produto e o número da loja do produto mais caro.

147. $\bigstar\bigstar\bigstar$ Crie um algoritmo para gerenciar um sistema de reservas de mesas em uma casa de espetáculo.

     A casa possui 30 mesas de 5 lugares cada. O algoritmo deverá permitir que o usuário escolha o código da mesa (100 a 129) e forneça a quantidade de lugares desejados. O algoritmo deverá informar se foi possível realizar a reserva e atualizar a reserva. Se não foi possível, o algoritmo deverá emitir uma mensagem. O algoritmo deverá terminar quando o usuário digitar o código 0 (zero) para uma mesa ou quando todos os 150 lugares estiverem ocupados.

148. $\bigstar\bigstar$ Em um concurso público inscreveram-se 5000 candidatos para 100 vagas. Cada candidato fez 3 provas, tendo cada prova pesos 2, 3 e 5, respectivamente, na ordem em que foram feitas. Fazer um algoritmo que leia nome, matrícula e os pontos obtidos pelos candidatos em cada prova. Apresentar também a classificação, a matrícula e o nome dos candidatos aprovados, ordenados pela classificação.

149. $\bigstar\bigstar$ Dado o seguinte vetor:
     $$VET = \left[\begin{array}{cccccccc} 3 & 2 & 4 & 1 & 2 & 5 & 8 & 3 \end{array} \right]$$

     Qual será a sua configuração depois de ser executado os comandos:

     para I de 8 ate 5 passo -1 faca
       AUX <- VET[I]
       VET[I] <- VET[8-I+1]
       VET[8-I+1] <- AUX
     fimpara
     VET[3] <- VET[1]
     VET[VET[3]] <- VET[VET[2]]
     

150. $\bigstar\bigtar$ Dado o seguinte vetor de caracteres:
     $$VET = \left[\begin{array}{c\vert c\vert c\vert c\vert c\vert c\ve... ... c} \hline T & R & X & S & & E & O & B & A & ! \hline \end{array} \right]$$

     Qual será a sua configuração depois de ser executado os comandos:

      AUX <- VET[6]
      VET[6] <- VET[9]
      VET[9] <- AUX
      para I de 1 ate 4 passo 1 faca
       AUX <- VET[I]
       VET[I] <- VET[9-I]
       VET[9-I] <- AUX
      fimpara
      VET[6] <- VET[2]
     

151. $\bigstar\bigstar$ Faça um programa que preencha um vetor com dez números inteiros e um segundo vetor com cinco números inteiros. O programa deverá mostrar uma lista dos números do primeiro vetor com seus respecticos divisores armazenados no segundo vetor, bem como suas posições.

     Ex:

     $$NUM = \left\vert\begin{array}{c\vert c\vert c\vert c\vert c\vert ... ...ine 5 & 12 & 4 & 7 & 10 & 3 & 2 & 6 & 23 & 16 \hline \end{array} \right\vert$$
     $$NUM = \left\vert\begin{array}{c\vert c\vert c\vert c\vert c}\hline 3 & 11 & 5 & 8 & 2 \hline \end{array} \right\vert$$

     Número 5

     Divisível por 5 na posição 3

     Número 12

     Divisível por 3 na posição 1

     Divisível por 2 na posição 5

     Número 4

     Divisível por 2 na posição 5

     Número 7

     Não possui divisores no segundo vetor

     Número 10

     Divisível por 5 na posição 3

     Divisível por 2 na posição 5

152. $\bigstar\bigstar$ Faça um programa que leia um conjunto de quinze valores e armazene-os em um vetor. A seguir, separe-os em dois outros vetores (P e I) com cinco posições cada. O vetor P armazena números pares e o vetor I, números ímpares. Como o tamanho dos vetores pode não ser suficiente para armazenar todos os números, deve-se sempre verificar se já estão cheios. Caso P ou I estejam cheios, deve-se mostrá-los e recomeçar o preenchimento da primeira posição. Terminado o processamento, mostre o conteúdo restante dentro dos vetores P e I.

153. $\bigstar\bigstar$ Faça um programa que leia dois vetores (A e B) com cinco posições para números inteiros. O programa deve, então subtrair o primeiro elemento de A do último elemento de B, acumulando o valor, subtrair o segundo elemento de A do penúltimo de B, acumulando o valor, e assim por diante. Ao final, mostre o resultado de todas as subtrações realizadas.

154. $\bigstar$ Faça um programa que leia um vetor com quize posições para números inteiros. Depois da leitura, divida todos os seus elementos pelo maior valor do vetor. Mostre o vetor após os cálculos.

     SOLUçãO: VMMAIORELEMENTODIV.C.

155. $\bigstar\bigstar\bigstar$ (Prova EST/2012-2) Escreva um programa em C que leia uma matriz A de tamanho 10 x 10 de caracteres. Faça uma busca nessa matriz e coloque as vogais que estejam localizadas na diagonal secundária dentro de um vetor B. Ao final, imprima apenas as vogais que foram gravadas nesse vetor.

     SOLUçãO: VMCONTAVOGAISMATRIZ.C.

156. $\bigstar\bigstar\bigstar$ (Prova EST/2012-2) Considere o trecho de código abaixo e responda ao que se pede:

     a) Qual deve ser o valor de x para que seja alocado um vetor de 10 posições? Justifique a sua resposta.

     b) Existe alguma hipótese de não ser possível alocar esse vetor? Justifique a sua resposta.

     int *v, x;
     
     v = (int *) malloc (x);
     

157. $\bigstar\bigstar\bigstar$ A distância entre várias cidades é dada pela tabela abaixo (em quilometros):

     ×	1	2	3	4	5
     1	00	15	30	05	12
     2	15	00	10	17	28
     3	30	10	00	03	11
     4	05	17	03	00	80
     5	12	28	11	80	00

     a) Construa um algoritmo que leia a tabela acima e informe ao usuário a distância entre duas cidades por ele requisitadas.

     b) Construa um algoritmo que leia a tabela acima e dado um determinado percurso, imprima o total percorrido.

     Exemplo: dado o percurso 1, 2, 3, 2, 5, 1, 4, teremos: 15 + 10 + 10 + 28 + 12 + 5 = 80 km.

158. $\bigstar\bigstar$ Escreva um algoritmo que armazene o nome e as notas das provas 1 e 2 de 15 alunos. O algoritmo depois deverá armazenar a média das notas de cada aluno e gravar também a situação de cada aluno. Considere que a nota mínima para aprovação é 6.0. Ao final, exibir os nomes e as notas dos alunos que foram aprovados.

159. $\bigstar\bigstar$ Elabore um algoritmo para criar um vetor de 30 posições com valores reais. As 15 primeiras posições serão informadas pelo usuário e as posições seguintes serão os números digitados pelo usuário, mas na ordem inversa. Ao final, o algoritmo deverá imprimir o vetor.

160. $\bigstar\bigstar$ Escreva um programa em C que leia uma matriz A quadrada de ordem 10. Em seguida, copie os valores da matriz A que são primos para um vetor B. Ao final, imprima o vetor B (apenas com os valores preenchidos).

161. $\bigstar\bigstar$ (Prova UEA/2013.2) Um professor precisa lançar a frequência de uma turma de Linguagem de Programação da EST. O professor possui uma planilha em papel com as presenças (P) e faltas (F) diárias para os 50 alunos da turma nos 30 dias de aula (cada dia de aula corresponde a duas frequências). Faça um programa em C para auxiliar o professor a obter as informações de que ele necessita. O programa deverá:

     a. Ler a planilha de frequência para uma matriz de caracteres de 50 x 30 (50 alunos e 30 dias).

     b. Escrever o total de faltas para cada um dos 50 alunos, informando caso esteja reprovado por falta (mais de 15 de faltas), conforme exemplo abaixo.

     Exemplo: Aluno 1: 12 faltas Aluno 2: 10 faltas Aluno 3: 2 faltas Aluno n: X faltas

     c. Informar o total de alunos reprovados por falta.

     d. Informar o dia em que houve a maior quantidade de faltas.

     e. Informar o dia em que houve a maior quantidade de presenças.

     SOLUçãO: VMPLANILHAFREQUENCIA.C.